computing with integrals in nonlinear algebra
March 9–25, 2021
A 6-lecture course virtually hosted by MPI-MiS in Leipzig and held on zoom
Interested participants should register with Pierre Lairez or Bernd Sturmfels.
The lecture is over, but the material stays here.
abstract
-
How to compute 100 digits of the volume of a semialgebraic (defined by polynomial inequalities)?
-
How to compute the moments $\int_{[0,1]^n} f(x_1,\dotsc,x_n)^k \mathrm{d}x_1 \dotsc \mathrm{d}x_n$ for large $k$? This problem stems from polynomial optimization.
-
How to compute a recurrence relation for the numbers $\sum_{k=0}^n \binom{n}{k}^2\binom{n+k}{k}^2$? This relation is central in Apéry’s proof of the irrationality of $\zeta(3)$.
-
How to count the number of smooth rational curves of degree $d$ on a smooth quartic surface in $\mathbb{P}^3$?
These questions from diverse area of mathematics all feature period functions of rational integrals: analytic functions defined by integrating multivariate rational functions. In some regards, period functions are the simplest nonalgebraic functions. One of the first instance to be studied was the perimeter of the ellipse, as a function eccentricity.
I will first expose the fundamental material to compute with period function: linear differential equations as a data structure, symbolic integration and numerical analytic continuation. Next, I will show how to apply these technique in practice on many different problems, including the four questions above. As much as possible, I will connect with current research questions.
schedule
lecture #1, tue 9 mar 2021, 15h-17h (UTC+1)
Introduction. Differentially finite functions. Diffential equations as datastructure. Diagonals of rational functions.
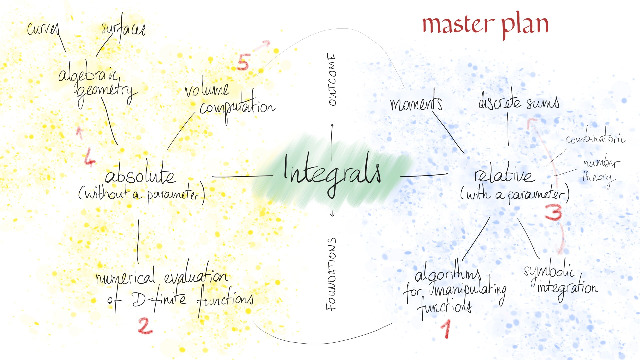
lecture #2, thu 11 mar 2021, 15h-17h (UTC+1)
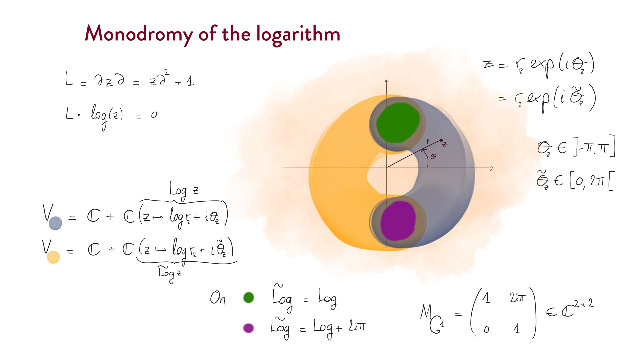
Local study of D-finite functions. Monodromy. Numerical evaluation of differentially finite functions. Computation of partial Taylor sums. Binary splitting.
lecture #3, tue 16 mar 2021, 15h-17h (UTC+1)
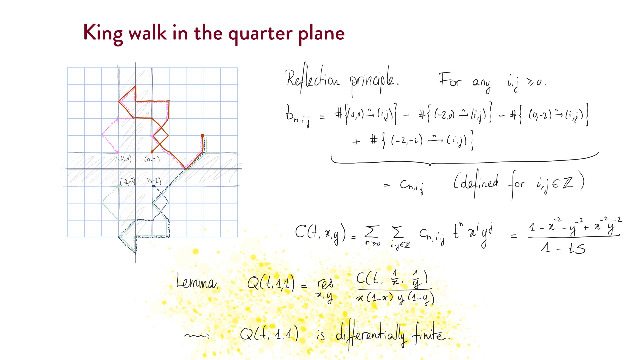
Diagonals, constant terms and residues of rational functions. Binomial sums. D-finitess for these functions. Arithmetic properties.
lecture #4, thu 18 mar 2021, 15h-17h (UTC+1)

Periods in experimental mathematics. Computation of the Picard group of a quartic surface.
lecture #5, tue 23 mar 2021, 15h-17h (UTC+1)

Volume of semialgebraic sets. Method of moments.
lecture #6, thu 25 mar 2021, 15h-17h (UTC+1)
Problem solving. Please have Sagemath and ore_algebra installed.
references
A selection of articles that roughly define the scope of this lecture.
-
Bostan, A., Lairez, P. and Salvy, B. (2017) ‘Multiple binomial sums’, Journal of Symbolic Computation, 80, pp. 351–386.
-
Griffiths, P. A. (1969) ‘On the periods of certain rational integrals’, Annals of Mathematics, 90, pp. 460–541.
-
Hoeven, J. van der (2001) ‘Fast evaluation of holonomic functions near and in regular singularities’, Journal of Symbolic Computation, 31(6), pp. 717–743.
-
Lairez, P. (2016) ‘Computing periods of rational integrals’, Mathematics of Computation, 85(300), pp. 1719–1752.
-
Lairez, P., Mezzarobba, M. and Safey El Din, M. (2019) ‘Computing the volume of compact semi-algebraic sets’, ISSAC 2019.
-
Lairez, P. and Sertöz, E. C. (2019) ‘A numerical transcendental method in algebraic geometry’, SIAM Journal on Applied Algebra and Geometry, pp. 559–584.
-
Lasserre, J. B. (2019) ‘Volume of sublevel sets of homogeneous polynomials’, SIAM Journal on Applied Algebra and Geometry, 3(2), pp. 372–389.
-
Mezzarobba, M. (2016) ‘Rigorous multiple-precision evaluation of D-finite functions in Sagemath’.
-
Michałek, M. and Sturmfels, B. (2021), Invitation to nonlinear algebra
-
Molin, P. and Neurohr, C. (2019) ‘Computing period matrices and the Abel-Jacobi map of superelliptic curves’, Mathematics of Computation, 88(316), pp. 847–888.
-
Oaku, T. (2013) ‘Algorithms for integrals of holonomic functions over domains defined by polynomial inequalities’, Journal of Symbolic Computation, 50, pp. 1–27.
-
Salvy, B. (2019) ‘Linear differential equations as a data structure’, Foundations of Computational Mathematics, 19(5), pp. 1071–1112.
-
Sturmfels, B. and Sattelberger, A.-L. ‘D-Modules and Holonomic Functions’
content
This is the plan. I will probably skip some subsections here and there, depending on the audience’s interests.
Linear differential equations as a data structure
- differentially finite (D-finite) power series
- equivalence with recurrence relation
- example of D-finite functions
- algebraic functions are D-finite
- examples from combinatorics
- elementary closure properties
- addition, multiplication, some forms of composition
- solutions to linear ODEs
- ordinary points
- singular points
- exponents
- regular singularities
- formal solutions
- proof of identity
- guessing
- software packages
- gfun (Maple)
- ore_algebra (Sagemath)
- integration of multivariate D-finite functions
Numerical evaluation of differentially finite functions
- radius of convergence of a D-finite power series
- computation of partial Taylor sums
- naive quadratic algorithm
- binary splitting
- numerical analytic continuation
- decomposition in elementary steps
- regular singular points
- rigorous error bounds
- tail bounds
- fixed point method
- example: computing π
Periods of rational integrals
- definition
- relation with homology and cohomology
- topological reduction of periods
- analytic reduction of periods
- period matrix
- periods depending on a parameter…
- … are D-finite (Picard-Fuchs equations)
- arithmetic properties
- Bombieri-Dwork conjecture
- examples
- formal periods and diagonals
- definition
- they satisfy a Picard-Fuchs equations
- further arithmetic properties
- Furtsenberg theorem
- Christol conjecture
- binomial sums
- integral representations
- application to symbolic summation
- computation of Picard-Fuchs equations
- regular case
- singular case
Period numbers of curves and surfaces
- periods of curves
- period matrix
- Torelli’s theorem
- computation
- periods of surfaces
- period matrix
- Torelli-type theorems
- computation
- effective Lefschetz (1,1)-theorem
- LLL
- separation of periods of quartic surfaces
- higher dimensions
- Hodge conjecture
Computation of volume of semialgebraic sets
- statement of the problem
- function «volume of a slice»
- it is a period of rational function!
- everything in this course applies!
- an actual algorithm
- computing volume using moments
- computing moments using Picard-Fuchs equations
- further thoughts (WIP)
Research directions
- faster algorithms for computing periods
- revisiting the holonomic D-module approach to integration